Convolution via cross approximation

Multidimensional convolution plays a crucial role in many applications. We have proposed a new method for approximate computation of the convolution in low-rank tensor formats that is based on the cross approximation in the frequency domain. The method is applicable to any SVD-based tensor format (skeleton, Tucker, Tensor Train, Hierachical Tucker). We have computed Newton potentials of different electronic densities, and also presented preliminary results for the solution of the Hartree-Fock equation on tensor product grids. For a practically interesting range of one-dimensional grid sizes \(n \sim 10^{3}-10^{5}\) our algorithm is faster.

He density	H2 density

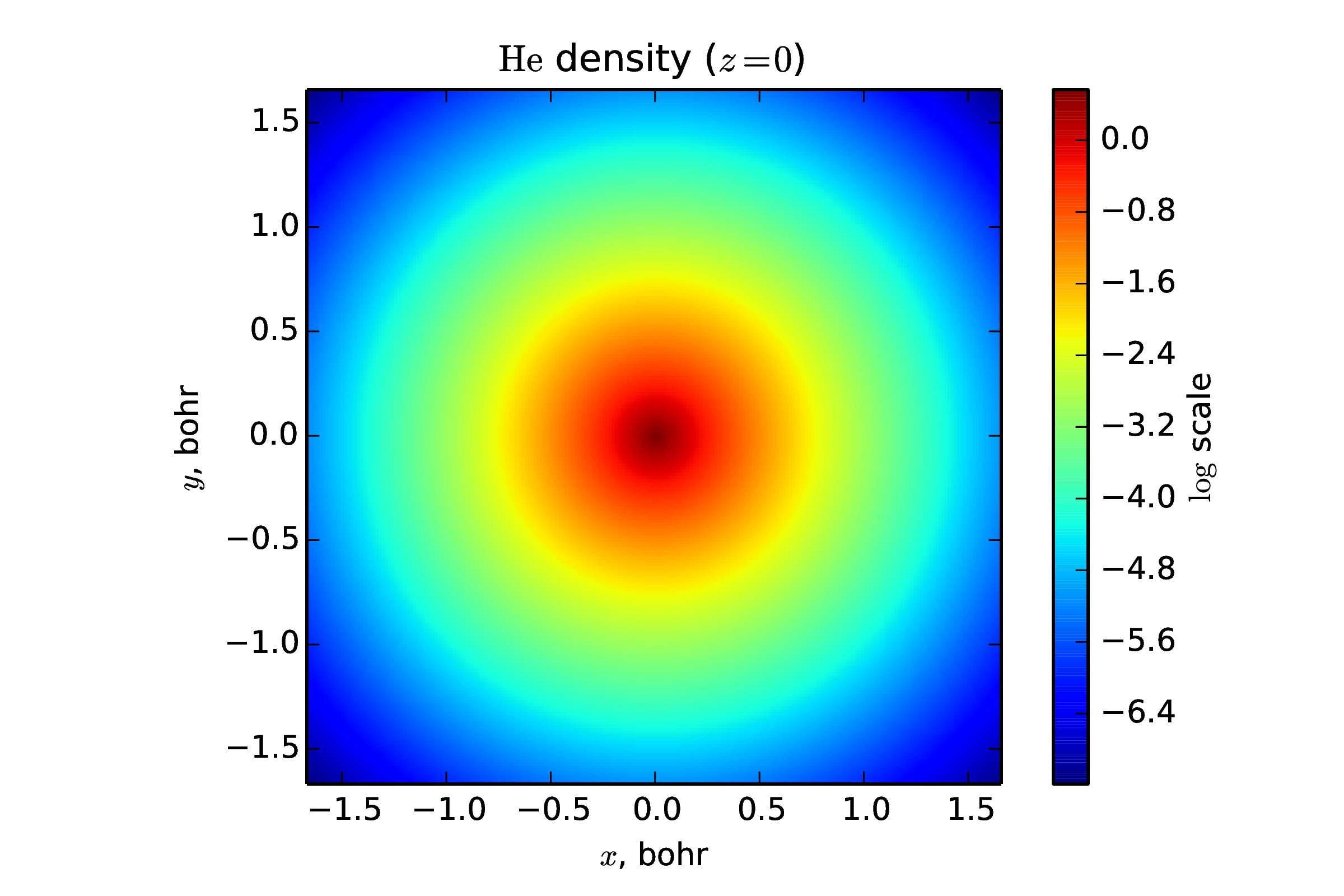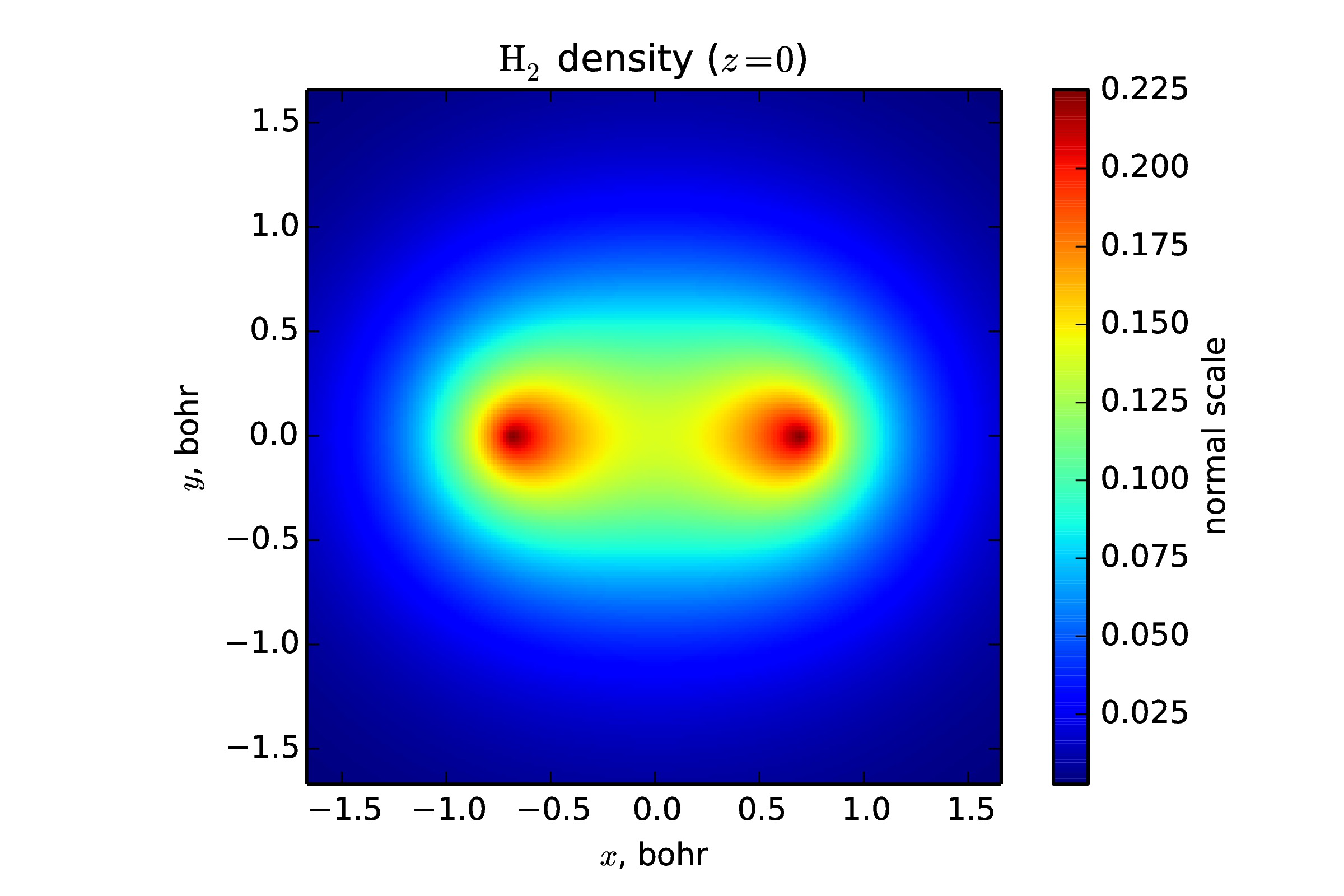• Preprint on arXiv
• MiniTucker Toolbox on Github
• Data from the paper on Bitbucket