Alternating low-rank method for the Lyapunov equation
13/10/2014
Time-stepping free method based on the rational Krylov subspaces play an important role in many applications. The adaptative selection of the shifts for the construction of the RKS is crucial. In this paper we propose a new algorithm for the selection of the shifts. It is based on the connection between the solution of the Lyapunov equation
$$
AX + XA^{\top} = y_0 y_0^{\top}
$$
and the solution of a linear ODE
$$
\frac{dy}{dt} = Ay, \quad y(0) = y_0.
$$
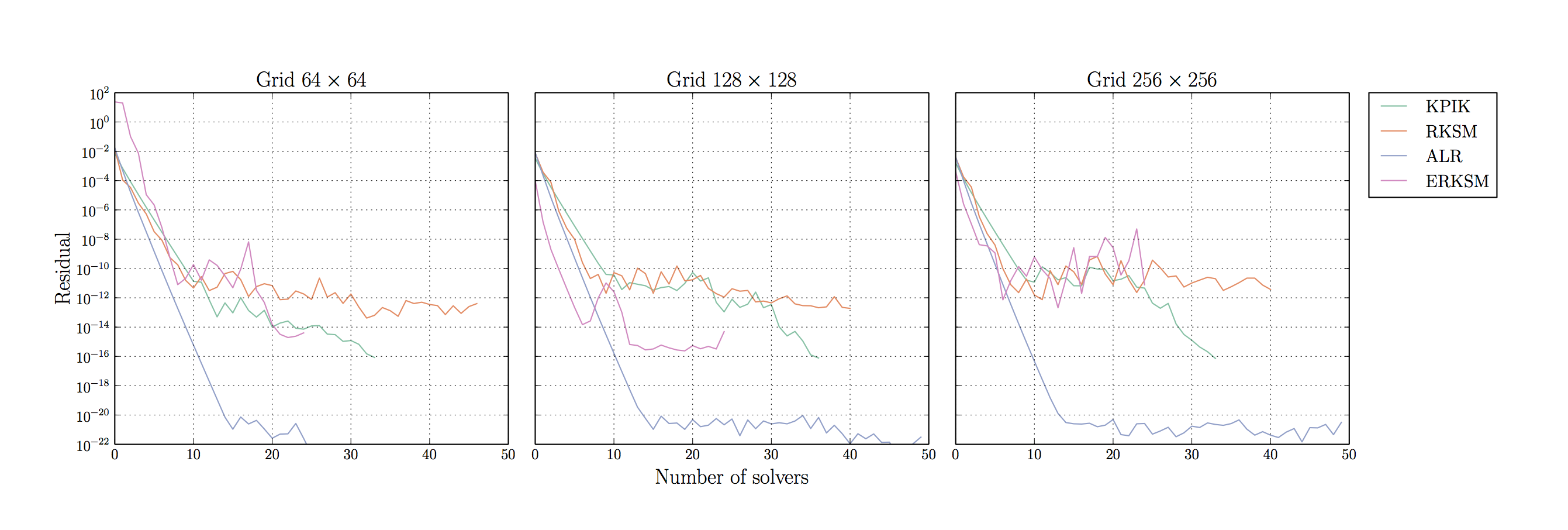
We have compared the efficiency of the new method with KPIK and RKSM methods (implementation were taken from the homepage of Valeria Simonchini. The ALR method we propose was the most efficient one (and it is parameter-free).
