Convergence analysis of a projected fixed-point iteration
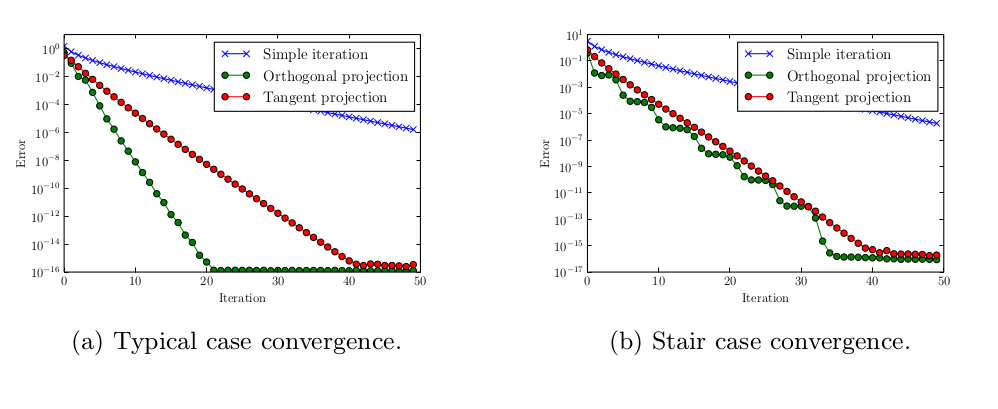
In this paper by Denis Kolesnikov and Ivan Oseledets we analyse convergence of projected fixed-point iteration on a Riemannian manifold of matrices with fixed rank. As a retraction method we use `projector splitting scheme’. We prove that the projector splitting scheme converges at least with the same rate as standard fixed-point iteration without rank constraints. We also provide counter-example to the case when conditions of the theorem do not hold. Finally we support our theoretical results with numerical experiments.
The most interesting finding is the splitting of the error into two components: normal component and tangent component. The normal component shows staircase convergence which “feels” the curvature, but this convergence is much faster, thus the total error does not show it.