A TT-eigenvalue solver that finally works
In a recent preprint by Maxim Rakhuba and Ivan Oseledets we propose a new algorithm for calculation of vibrational spectra of molecules using tensor train decomposition. Under the assumption that eigenfunctions lie on a low-parametric manifold of low-rank tensors we introduce the concept of manifold preconditioning of well-known iterative methods …
more ...Exponential machines and tensor trains
Modeling interactions between features improves the performance of machine learning solutions in many domains (e.g. recommender systems or sentiment analysis). In this paper, we introduce Exponential Machines (ExM), a predictor that models all interactions of every order. The key idea is to represent an exponentially large tensor of parameters …
more ...Convergence analysis of a projected fixed-point iteration
In this paper by Denis Kolesnikov and Ivan Oseledets we analyse convergence of projected fixed-point iteration on a Riemannian manifold of matrices with fixed rank. As a retraction method we use `projector splitting scheme’. We prove that the projector splitting scheme converges at least with the same rate as standard …
more ...Compress-and-eliminate solver for sparse matrices
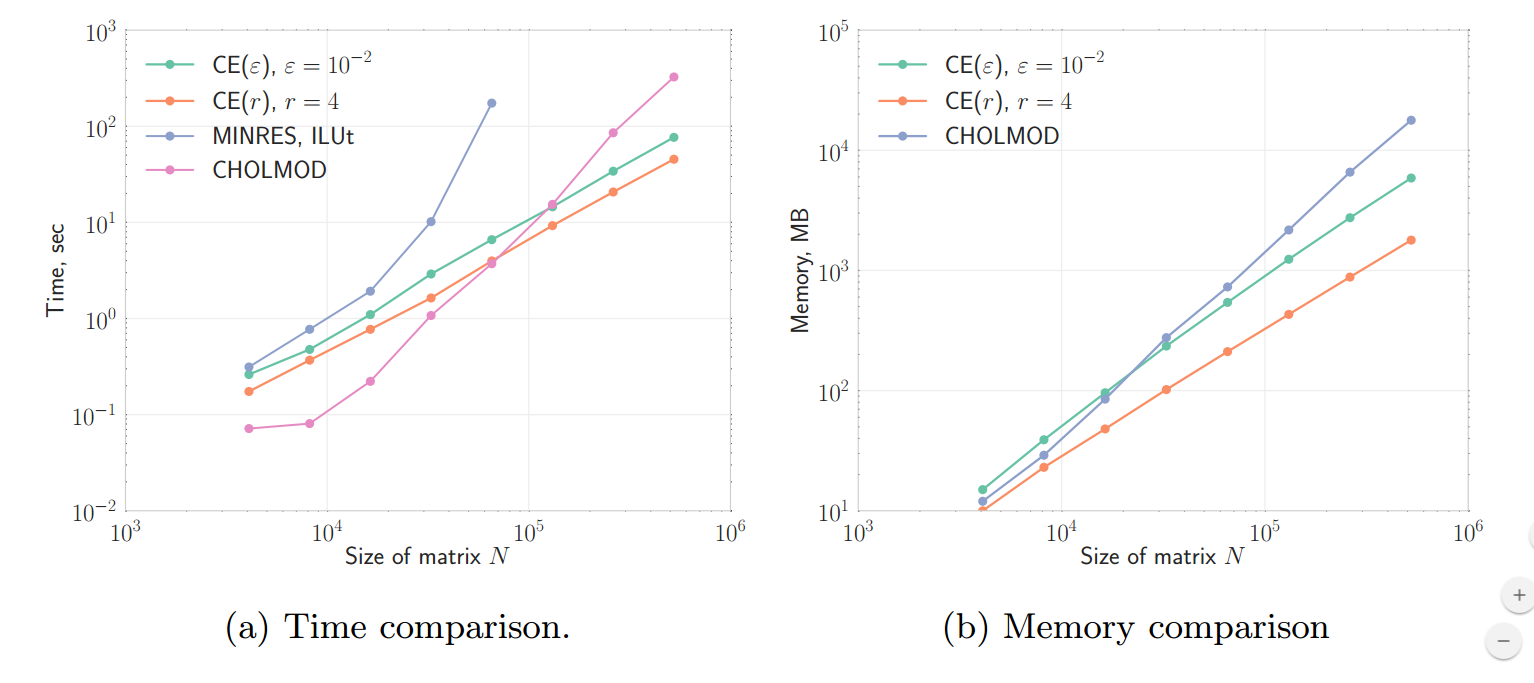
We propose a new Compress-and-Eliminate Solver for sparse matrices. The approach is proposed by Daria Sushnikova and Ivan Oseledets. The solver has a very simple algebraic structure, and outperfoms state-of-the art CHOLMOD software.
New paper in SIMAX
Our paper on a new rational Krylov method for solving large-scale Lyapunov equations “From Low-Rank Approximation to a Rational Krylov Subspace Method for the Lyapunov Equation” by D. Kolesnikov and I. Oseledets is now published in SIAM Journal oon Matrix Analysis and Applications
more ...New paper in J. Comp. Phys
Our paper on low-rank computation of huge-dimensional path integrals “A low-rank approach to the computation of path integrals” by M. S. Litsarev and I. Oseledets published in Journal of Computational Physics
more ...New paper in J. Chem. Phys
Our paper on multidimensional potential energy surfaces approximation] using a combination of active subspace methods and tensor train decomposition “Fitting high-dimensional potential energy surface using active subspace and tensor train (AS+TT) method” by V. Baranov and I. Oseledets is now published in Journal of Chemical Physics
more ...Anton Sukhinov leaves the group
Our research scientist Anton Sukhinov has finished working at Scientific Computing group. We thank Anton for his valuable contributions to the research agenda and for his work with the industrial partners (Huawei, Intel) and wish him good luck in his future career.
more ...MMMA-2015
We have succesfully hosted at Skoltech 4-th international conference on Matrices in Mathematics and Applications, MMMA-2015. More than 100 talks from 6 countries and 10 universities. This is the first conference at our new building of such, and we had many interesting talks and discussions. The talks and videos …
more ...Path integrals & low-rank for unbounded domains
Path integrals play a dominant role in description of a wide range of problems in physics and mathematics. They are a universal and powerful tool for condensed matter and high-energy physics, theory of stochastic processes and parabolic differential equations, financial modelling, quantum chemistry and many others.
The solution of the …
more ...Cross-conv paper published!
Our cross-convolution paper “Fast Multidimensional Convolution in Low-Rank Tensor Formats via Cross Approximation” by M. Rakhuba, I. Oseledets is now published in SIAM Journal on Scientific Computing
more ...Similarity for heterogeneous networks
We propose a generalization of SimRank similarity measure for heterogeneous information networks. Each node is associated with a set of objects and there are different possible relations. This is encoded into the adjacency tensor, and the TensorSimRank equation is given as
Time integration of tensor trains published!
Our paper on time integration of tensor trains “Time integration of tensor trains” by C. Lubich, I. Oseledets, B. Vandereycken is now published in SIAM Journal on Numerical Analysis
more ...Maximum-volume principle for rectangular matrices
A definition of p-volume of rectangular matrices is given. We generalize the results for square maximum-volume submatrices to the case rectangular maximal-volume submatrices and provide estimates for the growth of the coefficients. Three promising applications of such submatrices are presented: recommender systems, finding maximal elements in low-rank matrices and preconditioning …
more ...Alexander Mikhalev defends his PhD
Congratulations to Alexander Mikhalev for his successful PhD defense in INM RAS!
more ...Convolutional neural networks and tensors
Deep learning is a huge topic today; speeding up the computation with convolutional neural network is crucial for fast classification. In this work we show how fine-tuned canonical polyadic (CP) decomposition can be used to speedup CNN by a factor of 8-10.
more ...This is a new page
The website is finally online!
more ...Alternating low-rank method for the Lyapunov equation
Time-stepping free method based on the rational Krylov subspaces play an important role in many applications. The adaptative selection of the shifts for the construction of the RKS is crucial. In this paper we propose a new algorithm for the selection of the shifts. It is based on the connection …
more ...Time evolution and optimization with MPS
The projector-splitting scheme in the TT/MPS format is a natural way to computing dynamics of quantum spin systems Hamiltonians with long-range interaction. We have proposed a unified approach that leads to a cheap and efficient computational scheme that can be applied to any Hamiltonian, represented in the MPO/TT …
more ...Time integration of tensor trains
Dynamical low-rank approximation is an efficient framework for solving continious and discrete-time problems in high-dimensions. Using the Dirac-Frenkel principle applied to the tensor-train format, we have propose a robust and efficient time integrator for the resulting system of nonlinear equations.
| Algorithm scheme | Approximate Laplace inversion |
|---|---|
 |
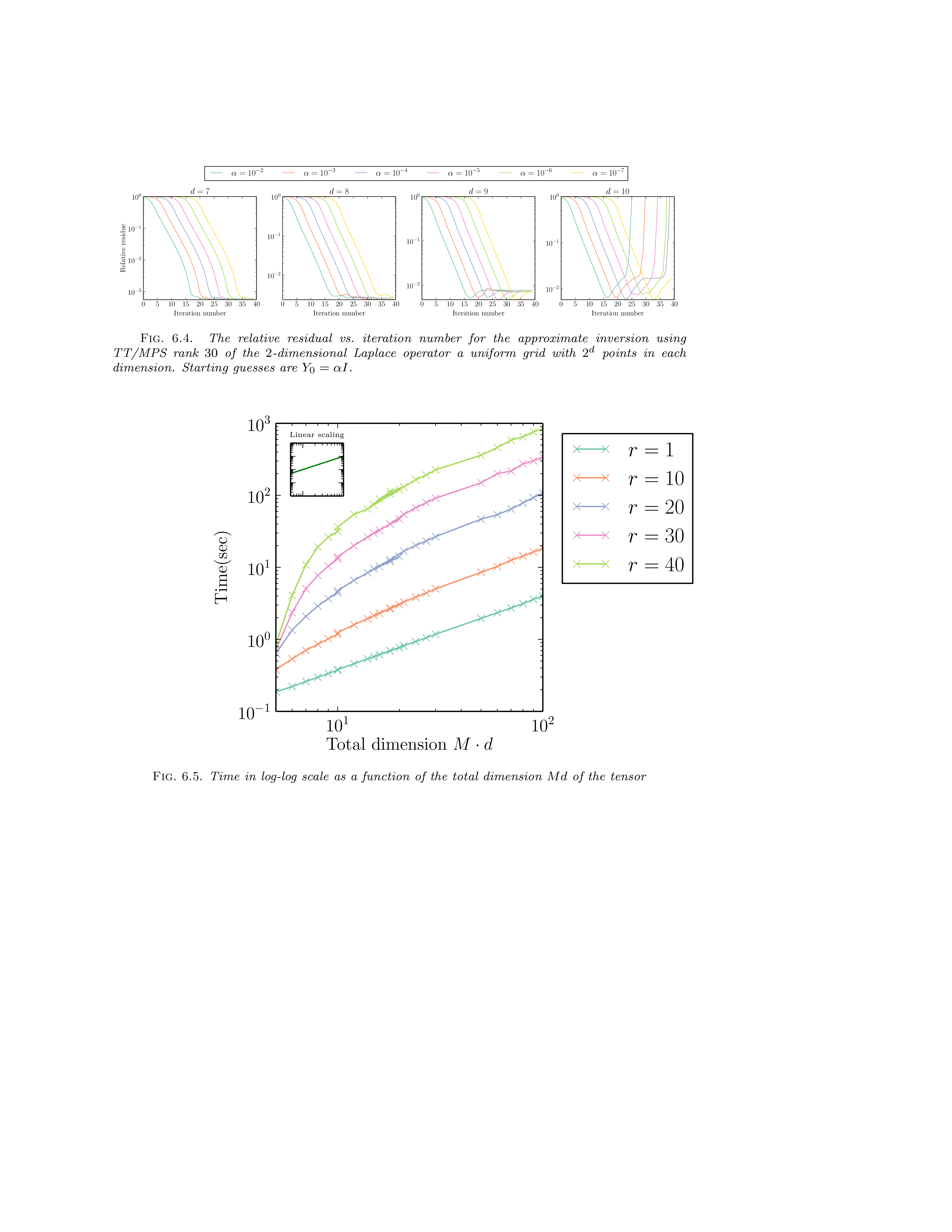 |
Multidimensional integrals in ion-atom collisions
Simulation in physics is full of multidimensional integrals. In the paper M. S. Litsarev and I. V. Oseledets. Low rank approximations for the DEPOSIT computer code. arXiv preprint 1403.4068, 2014 we consider the DEPOSIT code that is suited for the computation of ion-atomic collisons. The main computational bottleneck is …
more ...Preconditioners for hierarchical matrices
We continue to develop our h2tools package with the new functionality. The solution of linear systems with hierarchical matrices plays a crucial role in many applications. We use the sparse extended form of the H2-matrices to reduce the initial linear system to a block-structured linear system and then use this …
more ...Convolution via cross approximation
Multidimensional convolution plays a crucial role in many applications. We have proposed a new method for approximate computation of the convolution in low-rank tensor formats that is based on the cross approximation in the frequency domain. The method is applicable to any SVD-based tensor format (skeleton, Tucker, Tensor Train …
more ...Theses topics
I have put short descriptions of the available student project online. Please check
more ...Happy new year!
2013 is now in its full rights, so it is time to go on with research. With Christian Lubich we have finished a paper on a very efficient time-stepping scheme for the dynamical low-rank approximation —- so-called KLS-scheme, which is remarkably simple but efficient to compute the dynamics on low-rank …
more ...One more paper
One more old paper on explicit representations of simple functions in tensor formats is published in the Constructive Approximation!
more ...Solving parabolic systems (with application to Fokker-Planck)
Our paper on the new time-stepping scheme based on the QTT-format has been published in SISC!
more ...News
Four papers are in progress : on the block eigenvalue solver in the TT-format, on the dynamical low-rank approximation, on the tensor structure of the wavelet tensor train matrix and on the fast solution of the Stokes problem in tensor format. Hope to finish them soon.
Also, I put some …
more ...Publications of our group
We have recently put the publications of our research group at the Institute of Numerical Mathematics RAS on the web. The list is not yet full, but is close. Check it!
more ...Fast adaptive interpolation of multidimensional arrays in TT-format
This paper with Dmitry Savostyanov published in the end of 2011 in the Proceedings of 7th International Workshop on Multidimensional Systems (nDS), doi: 10.1109/nDS.2011.6076873 is about fast adaptive methods for the approximation of high-dimensional arrays by cross-type methods (such methods are quite popular for matrices).
The …
Dynamical TT-approximation
Dynamical low-rank approximation is a rather new and important topic, which was studied by Lubich and Koch for low-rank matrices and low-rank (in the sense of Tucker format) tensor decomposition. Such kind of techniques were well known in physics in chemistry, going back to Dirac-Frenkel principle, and MCTDH method for …
TT-Toolbox 2.2.
TT-Toolbox (TT=Tensor Train) Version 2.2
TT(Tensor Train) format is an efficient way for low-parametric
representation of high-dimensional tensors. The TT-Toolbox
is a MATLAB implementation of basic operations with
tensors in TT-format. It includes:
* tt_tensor and tt_matrix classes for storing vectors and operators
* Basic linear …
more ...Google My citations
Google mycitations service looks great. Here is mine
more ...I decided to by on a twitter also (now posts only in Russian, but who knows :) )
more ...Tensor-Train decomposition paper finally published!
Finally, after more than 2 years of reviewing process, the basic paper on the TT-format is published in SISC!
You can get the journal version here or directly at the SIAM website
The first text was based on the paper “Compact matrix form of the d-dimensional tensor decomposition”. However …
more ...Solution of linear systems in the TT-format
The new paper, S.V. Dolgov, I.V. Oseledets, Solution of linear systems and matrix inversion in the TT-format describes a DMRG-type method for the solution of linear systems with both the matrix and the tensor in the TT-format. The method is able to solve certain structured …
more ...TT-Toolbox 2.1
TT-Toolbox 2.1 is released. It contains several bug fixes. My great thanks to Sergey Dolgov for writing many important routines and to Vladimir Kazeev for providing his code for the construction of the QTT-representation of discrete Laplace operator (it can be done for extremely high dimensions in …
more ...TT-Toolbox 2.0
New version of TT-Toolbox is released.
TT Toolbox version 2.0 introduces several major innovations compared to version 1.0.
New classes tt_tensor and tt_matrix, which now represent TT-tensors and TT-matrices.
Object-oriented approach allowed to overload many standard MATLAB functions, including addition, subtraction,
multiplication by number, scalar …
DMRG+QTT
DMRG (Density Matrix Renormalization Group) is a very efficient algorithm for computation of low-lying eigenstates of quantum spin systems. QTT (Quantics Tensor Train) consists in tensorization of one-dimensional objects (i.e. vectors of values of function on a grid with 2^d points) into a d-dimensional tensor, and application of …
more ...Tensor Train in a nutshell
I have written a one-page article that describes vital operations in TT-format. Hope you will find it convincing, that TT-format is indeed a very elegant representation for tensors.
more ...Relation of tensors, quantics TT and wavelet tensor trains
In our paper Algebraic wavelet transform via quantics tensor train decomposition we show, how quantics tensor train approach, which consists in tensorization of vectors and matrices, can be interpreted as algebraic wavelet transform. Advantages are especially clear for two dimensional functions. Besides new results, this approach, called WTT (wavelet tensor …
more ...Preprint 2010-04: Explicit tensor-train representation of certain functions
The aim of Preprint 2010-04 is to construct explicit tensor-train representations for certain function-related tensors and vectors, which are constructed on the basis of introduced functional tensor train decomposition.These results are then used to construct explicit quantics tensor train decomposition for polynomial and sine functions.
more ...Krylov methods for tensors
Using Wedderburn rank-reduction formulae (for reference what is that, please read a nice paper by Gene Golub and Moody Chu) , we managed to create several robust Krylov methods for the approximation of three-dimensional tensors. It is a preprint 2010-1 of Institute of Numerical Mathematics. A new general interpretation is given …
more ...Tensor trees and tensor trains
In a new paper, we expose connections between tensor networks and recent recursive representations of high-dimensional tensors described by binary tensor trees and based on a sequence of skeleton (dyadic) decompositions for special unfolding matrices for a given tensor.    As the main result, we prove that …
more ...Black box cross approximation for multidimensional arrays
In our new paper, “TT cross approximation for multidimensional arrays” a new formula is presented for the recovery of a high-dimensional array from a part of its entries, provided that the array possesses some low-rank structure, namely it has small compression ranks (for example, a tensor of low canonical rank …
more ...TT toolbox
A first version of TT toolbox for MATLAB is released. It seems to works also under Octave —- through not fully tested. Any comments, suggestions and bug reports are welcome at ivan.oseledets(dog)gmail.com
All basic algorithms are implemented as a set of short MATLAB functions. You can try …
more ...Excluded sums and quasiseparable matrices.
The idea of Edelman et al. (published in 2005 in SIAM News) for fast evaluation of excluded sums and their relation with the non-recursive multipole method was largely unnoticed. The authors promised to give a new implementation of the multipole method based on their (quite elegant) approach however up to …
more ...Tensors inside of matrices give logarithmic complexity
The recently intoduced TT-format finds a surprising application for the compression of ordinary “two” or “three” dimensional matrices, related to the discretization of operators on tensor grids. For some examples the complexity is shown to be logarithmic in the matrix order. The new format (named TTM format) can be …
more ...New tensor decomposition
A new paper, A compact matrix form of the d-dimensional tensor decomposition is added. A new version of the TT (name is now not coming from “Tree Tucker”, but from “Three dimensional Tensors” which are the defining parameters of the format) format is presented, which is much simpler than the …
more ...Breaking the curse of dimensionality
In our new publication, “Breaking the curse of dimensionality, or how to use SVD in many dimensions” we present a simple recursive decomposition for multidimensional functions, operators, vectors and matrices. We prove that in the case when the canonical decomposition exists our new Tree-Tucker decomposition also exists with the same …
more ...How to find a good submatrix
Check out our new paper, “How to find a good submatrix” . It contains the description of an algorithm to find the well-conditioned submatrix in a given matrix. This algorithm plays a crucial role in our low-rank approximation methods, both for matrices and tensors. [drain file 2 url Matlab code is …
more ...Working with tensor-structured matrices and vectors
A new publication on tensor-structured matrices, with a tentative title “Linear algebra for tensor problems” is added. It is submitted to the special issue of Computing.
This paper is about structured iterations with matrices of low tensor rank in three dimensions. We show that in three dimensions we can use …
more ...One more paper on polynomials
Added a paper “Improved n-term Karatsuba formulae in GF(2)” that contains improved (and without proof —- optimal!) formulae for multiplication of binary polynomials in GF(2). As noted in the end of this paper, the goal is not purely theoretic, but also practical —- these optimal formulae will be used for …
more ...Some news
A new publication has been added. To my knowledge, it is the first paper where nontrivial class of low-tensor rank matrices with inverses also of a low tensor rank is found. This class is also not very small and many useful matrices can be reduced to it.
At present, I …
more ...Contacts
You can always contact me by email:
ivan.oseledets DOG gmail.com.
more ...Publications
Started the creation
That is my personal webpage, and I started its creation in April, 2008. Hope it will be interesting to somebody
more ...| 26/05/2016 | A TT-eigenvalue solver that finally works | Papers |
| 12/05/2016 | Exponential machines and tensor trains | Papers |
| 06/04/2016 | Convergence analysis of a projected fixed-point iteration | Papers |
| 30/03/2016 | Compress-and-eliminate solver for sparse matrices | Papers |
| 01/12/2015 | New paper in SIMAX | Papers |
Contact
We are located at the 2-nd floor of the new "Technopark-3” building in Skolkovo (few kilometers outside Moscow Ring Road). The building is accessible from Skolkovo Road (Сколковское шоссе) and Minskoe Highway (Минское шоссе).
email: